Ep 6. Visualizing Quantum Entanglement and Teleportation with Qiskit

Quantum entanglement and teleportation are fascinating phenomena in the world of quantum mechanics. They involve the mysterious connection between particles and the ability to transport information without physical movement. In this blog post, we will explore these two fundamental concepts, provide a simple example of quantum teleportation using Qiskit, and help you understand how entanglement enables the teleportation of quantum information across space.

Quantum Entanglement - Connecting Quantum States

Quantum entanglement is a peculiar phenomenon that connects the quantum states of particles, regardless of their distance from each other. When particles become entangled, measuring one will instantaneously affect the other, even if they are light-years apart. This bizarre behavior, coined by Einstein as “spooky action at a distance,” challenges our classical understanding of physics.

Now we will setup a quantum connect by generate an entangled pair of qubits. First, we need to initalize a circuit of two qubits.

import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, execute, BasicAer, IBMQ
from qiskit.visualization import plot_histogram, plot_bloch_multivector,plot_bloch_vector
from qiskit import *
import matplotlib.pyplot as plt
%matplotlib inline
from qiskit.visualization import plot_histogram

alice = QuantumRegister(1, name='Alice')
bob = QuantumRegister(1, name='Bob')

qc = QuantumCircuit(alice,bob)
qc.draw('mpl')

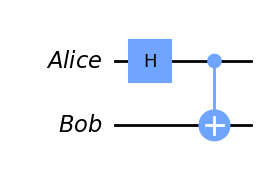
Then, we apply H gate and CNOT gate to make an entangled pair.

qc.h(alice[0])
qc.cx(alice[0],bob[0])
qc.draw('mpl')

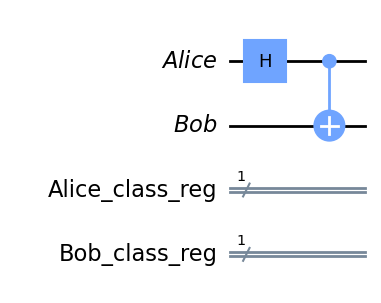
Don’t forget to add classical registers to store the measurement of these two qubits.

alice_classical_reg = ClassicalRegister(1,'Alice_class_reg')
bob_classical_reg = ClassicalRegister(1,'Bob_class_reg')

qc.add_register(alice_classical_reg)
qc.add_register(bob_classical_reg)
qc.draw('mpl')

Now, we can measure the values of these qubits

qc.measure(alice[0],alice_classical_reg)
qc.measure(bob[0],bob_classical_reg)
qc.draw('mpl')

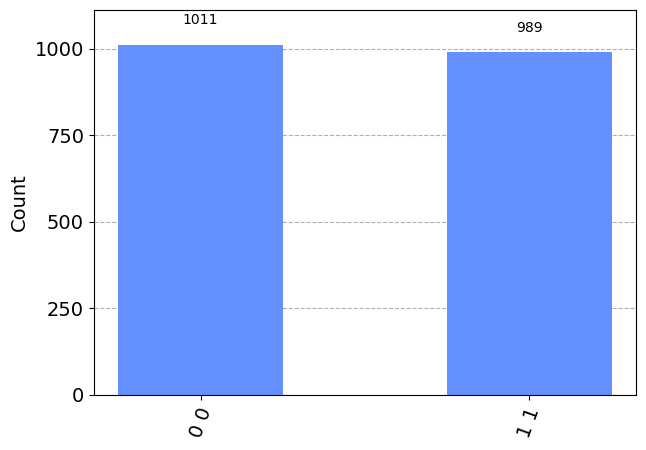
Due to quantum entanglement effect, we can see that these two qubits end up with $|00>$ or $|11>$ with 50-50 possibility.

backend = BasicAer.get_backend('qasm_simulator')
res = execute(qc, backend,shots =2000).result()
plot_histogram( res.get_counts())

Quantum Teleportation

Building upon the concept of entanglement, we have quantum teleportation. Quantum teleportation is a process that enables the transfer of a quantum state from one location to another, without the qubit itself moving through the intervening space. This phenomenon relies on the curious logic of quantum mechanics and has powerful implications for quantum communication.

Understanding Quantum Teleportation

The goal of quantum teleportation is to reliably transport an unknown quantum state from one place to another. It utilizes a pair of entangled qubits and classical communication to achieve this feat.

The basic steps involved are:

1. A pair of entangled qubits (1 and 2) is generated and qubit 2 is given to a recipient Bob.

2. The sender Alice has some unknown qubit (qubit 0) that she wants to teleport to Bob.

3. Alice performs a joint measurement on qubit 0 and qubit 1, which collapses their states based on the rules of quantum mechanics.

4. Alice sends the classical measurement results to Bob through a regular communication channel.

5. Depending on the message from Alice, Bob performs appropriate gate operations on qubit 2 to reconstruct the state of qubit 3.

Voila! The unknown quantum state has been teleported from Alice to Bob.

Simulating Quantum Teleportation with PennyLane

Step 0: First, we need to initialize the system with 3 qubits and 2 classical registers

target_info = QuantumRegister(1, name='target_info')
alice = QuantumRegister(1, name='Alice')
bob = QuantumRegister(1, name='Bob')

qc = QuantumCircuit(target_info,alice,bob)
alice_classical_reg = ClassicalRegister(1,'Alice_class_reg')
bob_classical_reg = ClassicalRegister(1,'Bob_class_reg')

qc.add_register(alice_classical_reg)
qc.add_register(bob_classical_reg)
qc.draw('mpl')

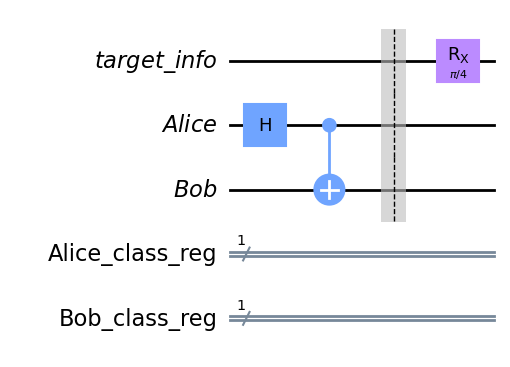
Step 1: Then, we create a pair of entangled qubits.

One is hold by Alice, another is hold by Bob

qc.h(alice[0])
qc.cx(alice[0],bob[0])
qc.draw('mpl')

Step 2: After that, at the sender side, we prepare a quantum state that we want to send to Bob.

For example, here we have state to send

plot_bloch_vector([1, np.pi/4, -np.pi/2], coord_type='spherical')

qc.barrier()
qc.rx(np.pi/4,0)
qc.draw('mpl')

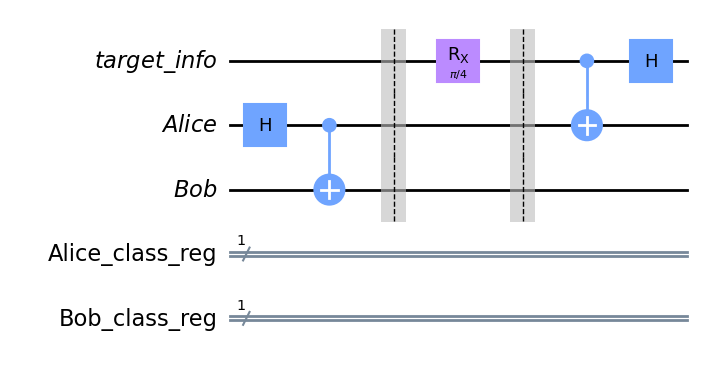
Step 3: Next, Alice applies targeted quantum state to her qubit

qc.barrier()
qc.cx(target_info[0],alice[0])
qc.h(target_info[0])
qc.draw('mpl')

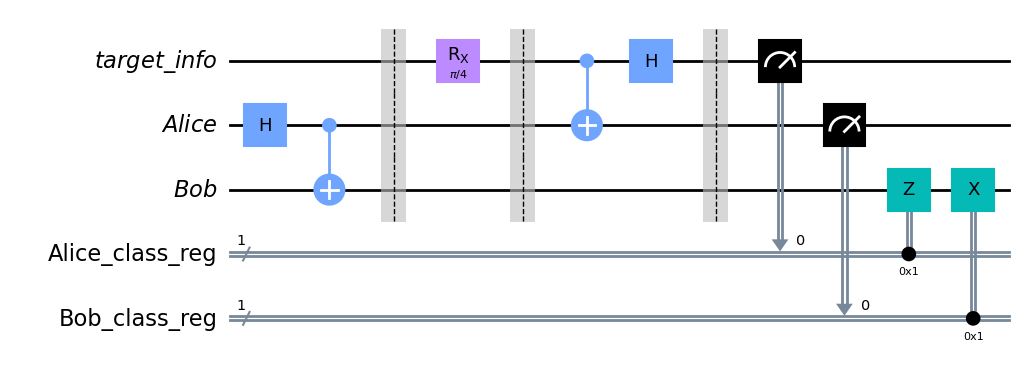
Step 4 : Alice measures state of qubits, stores results in classical bits and sends it to Bob

qc.barrier()
qc.measure(target_info[0],alice_classical_reg)
qc.measure(alice[0],bob_classical_reg)
qc.draw('mpl')

Step 5 : Bob Decodes based on bits he receives

qc.z(bob[0]).c_if(alice_classical_reg, 1)  #if alice_classical_reg is 1 apply Z gate
qc.x(bob[0]).c_if(bob_classical_reg, 1) #if bob_classical_reg is 1 apply x gate
qc.draw('mpl')

backend = BasicAer.get_backend('statevector_simulator')
out_vector = execute(qc, backend).result().get_statevector()
plot_bloch_multivector(out_vector)

Then, the state is successfully sent to Bob