Ep 7. Introduction to BB84 Quantum Key Distribution

In quantum cryptography, BB84 is a well-known protocol for secure key distribution between two parties. It relies on the principles of quantum mechanics to ensure the security of the exchanged key. At the core of BB84 are four important quantum states and two measurement bases- the Z-axis and the X-axis.

Why we need Quantum Key Distribution?

While current encryption methods such as RSA and elliptic curve cryptography provide robust security, they rely on the assumption that certain mathematical problems are hard to solve. However, the advent of quantum computing threatens to undermine this security, as algorithms like Shor’s algorithm could break these cryptosystems. This presents a significant risk to sensitive data, including financial records, medical information, and government communications.

Quantum Key Distribution (QKD) offers a solution by leveraging the principles of quantum mechanics rather than relying on computational complexity. By exploiting the properties of quantum mechanics, QKD enables the generation and distribution of truly random secret keys, impervious to even the most advanced quantum computers.

The Four Important States in BB84

In BB84, four quantum states are utilized for encoding information:

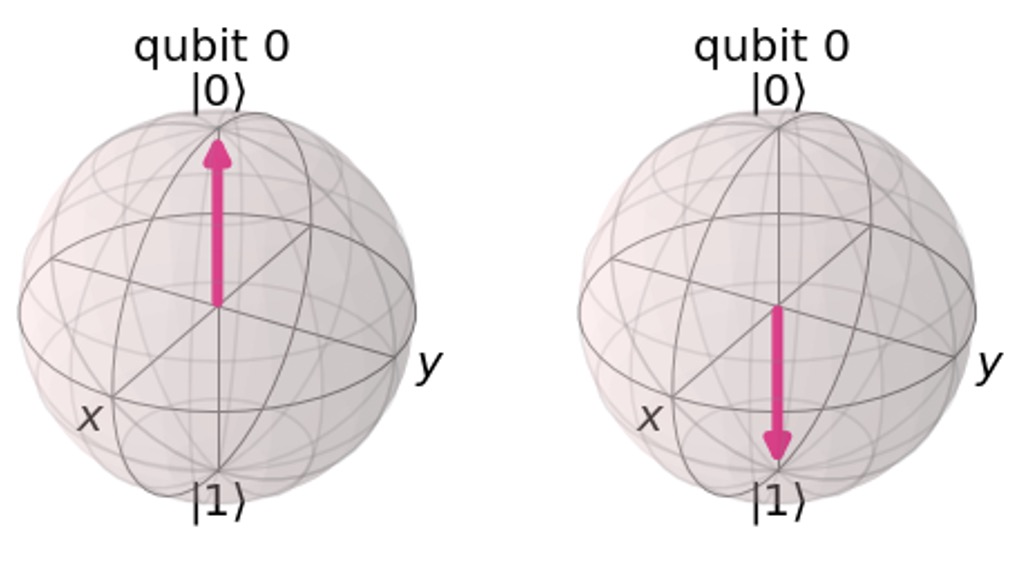
\(|0\rangle , |1\rangle\) are the standard basis states representing classical bits 0 and 1, respectively.

Fig 1: An illustration of quantum states $|0\rangle , |1\rangle$.

\(|+\rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle), |-\rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\) are superposition states, also known as the Hadamard basis states.

Fig 2: An illustration of quantum states $|+\rangle , |-\rangle$.

Measurement Basis: Z Axis and X Axis

In BB84, measurements are performed using two orthogonal bases: the Standard Basis and the Hadamard basis. These bases are represented by the measurement along the Z-axis and the X-axis, respectively.

Standard Basis: Measurements along the Z-axis correspond to the standard basis. In this basis, the states \(|0\rangle , |1\rangle\) are distinguished.

Hadamard Basis: Measurements along the X-axis correspond to the Hadamard basis. In this basis, \(|+\rangle , |-\rangle\) are map to 0 and 1, respectively.

Consequences of Measuring on the Wrong Axis

If a measurement is performed on the wrong axis, the result can be unpredictable and may lead to errors in decoding the key. For example, if a qubit encoded in the \(|+\rangle\) state is measured in the Z-axis instead of the X-axis, it collapses randomly to either 0 or 1 with equal probability. Similarly, measuring a qubit in the \(|1\rangle\) state in the X-axis would result in a random collapse to either 0 or 1.

BB84 leverages this effect to detect eavesdroppers on quantum channel.

BB84 Protocols

In BB84, original data is encrypted and shared on classical communication channels. The key is shared on quantum channel for decrypting the encrypted data.

Fig 3: QKD model.

The BB84 protocol is:

1. Key Generation: Alice prepares a random sequence of bits and encodes each bit using one of the four BB84 states. She then sends the encoded qubits to Bob over a quantum channel.

2. Measurement: Bob randomly chooses a basis (either Z-axis or X-axis) to measure each qubit he receives from Alice.
3. Public Discussion: Alice and Bob publicly announce which basis they used for each qubit without revealing the actual measurement results.
4. Error Check: Alice and Bob publicly compare a subset of their measurement bases. If they used the same basis for a given qubit, they expect the outcome to match. Any discrepancies indicate a potential error or eavesdropping attempt.
5. Key Distillation: After error checking, Alice and Bob discard the qubits measured in the wrong basis and use the remaining bits to generate a shared secret key.

For example: With a random sequence 0,0,1,0,1,0,1,0,1, and use half of bits whose bases are matched to detect eavesdropper.

	Bit 1	Bit 2	Bit 3	Bit 4	Bit 5	Bit 6	Bit 7	Bit 8	Bit 9
Alice’s sequence	0	0	1	0	1	0	1	0	1
Alice Axis	X	Z	X	Z	X	Z	Z	X	Z
Alice State	|+>	|0>	|->	|0>	|->	|0>	|1>	|+>	|1>
Bob Axis	Z	Z	Z	Z	X	X	X	X	Z
Bob Received Bits	1	0	1	0	1	1	0	0	1
Bases Match	No	Yes	No	Yes	Yes	No	No	Yes	Yes
Eve detection	-	OK	-	OK	OK	-	-	-	-
Agreed Key	-	-	-	-	-	-	-	0	1

Here, if eavesdropper Eve exists, since Eve doesn’t know which basises Alice and Bob use before step 3, Alice’s random measurements collapse the Alice’s sending states. Thus, when Alice and Bob use bits 2, 4, and 5 as checking bits, collapsed states lead mis-matched information in either Bit 2, 4, or 5 with high probability.